Flow deflection in turbomachines is established by stator and rotor blades with prescribed geometry that includes inlet and exit camber angles, stagger angle,camberline, and thickness distribution. The blade geometry is adjusted to the stage velocity diagram which is designed for specific turbine or compressor flow applications. Simple blade design methods are available in the open literature (see References). More sophisticated and high efficiency blade designs developed by engine manufacturers are generally not available to the public. An earlier theoretical approach by Joukowsky [1] uses the method of conformal transformation to obtain cambered profiles that can generate lift force. The mathematical limitations of the conformal transformation do not allow modifications of a cambered profile to produce the desired pressure distribution required by a turbine or a compressor blade design. In the following, a simple method is presented that is equally applicable for designing compressor and turbine blades. The method is based on (a) constructing the blade camberline and (b) superimposing a predefined base profile on the camberline. With regard to generating a base profile, the conformal transformation can be used to produce useful profiles for superposition purposes. A brief description of the Joukowsky transformation explains the methodology of symmetric and a-symmetric (Cambered) profiles.

The transformation uses the complex analysis which is a powerful tool to deal with the potential theory in general and the potential flow in particular. It is found in almost every fluid mechanics textbook that has a chapter dealing with potential flow. While they all share the same underlying mathematics, the style of describing the subject to engineering students differ. A very compact and precise description of this subject matter is found in an excellent textbook by Spurk [2].

Conformal Transformation, Basics

Before treating the Joukowsky transformation, a brief description of the method
is given below. We consider the mapping of a circular cylinder from the z-plane onto the ζ-plane, Figure 9.1. Using a mapping function, the region outside the
cylinder in the z-plane is mapped onto the region outside another cylinder in
the ζ-plane. Let P and Q be the corresponding points in the z- and ζ-planes
respectively. The potential at the point P is

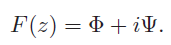
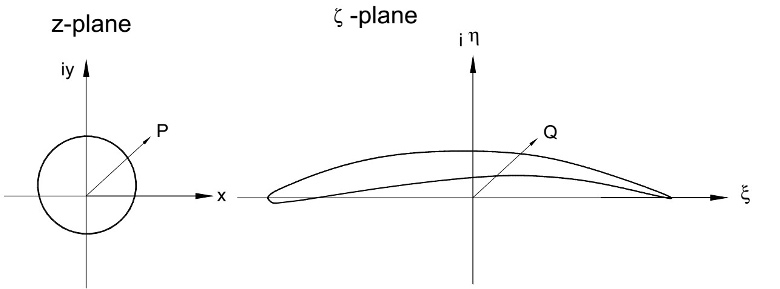
Figure 9.1: Conformal transformation of a circular cylinder onto an airfoil.

The point Q has the same potential, and we obtain it by insertion of the mapping function

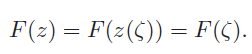
Taking the first derivative of Equation (9.2) with respect to ζ, we obtain the complex conjugate velocity ¯Vζ in the ζ plane from

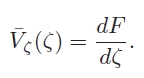
Considering z to be a parameter, we calculate the value of the potential at the point z. Using the transformation function ζ = f(z), we determine the value of ζ which corresponds to z. At this point ζ, the potential then has the same value as at the point z. To determine the velocity in the ζ plane, we form

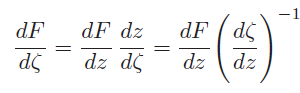
after introducing Equation (9.3) into Equation (9.4) and considering ¯ Vz(z) =dF/dz (9.4) is rearranged as

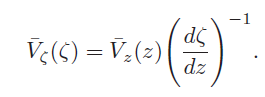
Equation (9.5) expresses the relationship between the velocity in ζ-plane and the one in z-plane. Thus, to compute the velocity at a point in the ζ-plane, we divide the velocity at the corresponding point in the z-plane by dζ/dz. The derivative dF/dζ exists at all points where dζ/dz = 0. At singular points with dzeta/dz = 0, the complex conjugate velocity in the ζ plane ¯ Vζ(ζ) = dF/dζ becomes infinite if it is not equal to zero at the corresponding point in the z-plane.

Joukowsky Transformation

The conformal transformation method introduced by Joukowski allows mapping an unknown flow past a cylindrical airfoil to a known flow past a circular cylinder. Using the method of conformal transformation, we can obtain the direct solution of the flow past a cylinder of an arbitrary cross section. Although numerical methods of solution of the direct problem have now superseded the method of conformal mapping, it has still retained its fundamental importance. In what follows, we shall examine several flow cases using the Joukowsky transformation unction: